RD Sharma Chapter 10 Class 9 Maths Exercise 10.3 Solutions is concerned with the Congruent Triangles. In this exercise, we will discuss the Criterion of Congruence – SAS (Side-Angle-Side). According to the criteria, if two sides and the interior angle of a triangle is equivalent to the corresponding sides and the interior angle of another triangle, then both triangles are assumed to be congruent. The solutions have been systematically planned for class 9 students to understand all chapter 10 Maths problems.
Moreover, RD Sharma Chapter 10 Class 9 Maths Exercise 10.3 Solutions PDF will help understand the level and varieties of problems asked in the exam. Practice with the PDF attached below with the stepwise explanations in an easy manner. Practicing regularly helps to score well in the exam.
Learn about RD Sharma Class 9 Chapter 10 Congruent of Triangles
Download RD Sharma Chapter 10 Class 9 Maths Exercise 10.3 Solutions PDF
Solutions for Class 9 Maths Chapter 10 Congruent Triangles Exercise 10.3
Important Definitions RD Sharma Chapter 10 Class 9 Maths Exercise 10.3 Solutions
In this exercise of Chapter 10, we will learn about the Criterion of Congruence – SAS ( Side-Angle-Side). Go down and look at the information regarding Criterion of Congruence – SAS ( Side-Angle-Side).
SAS ( Side-Angle-Side)
If any two sides and the angle comprised between the sides of one triangle are equal to the corresponding two sides and an angle among the sides of the second triangle, then the two triangles are assumed to be congruent by SAS ( Side-Angle-Side) rule.
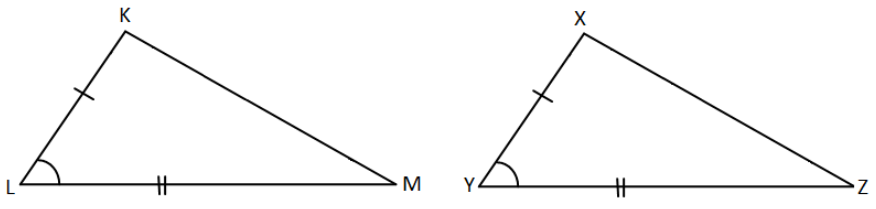
In the above-given figure,
= Here in ∆KLM and ∆XYZ,
= KL = XY, LM = YZ and ∠L = ∠Y
= Therefore, ∆KLM ≅ ∆XYZ.
Note: The composed angles need to be equivalent for congruency. If in the above figure, ∠L ≠ ∠Y and ∠L = ∠X, the triangle may not be congruent.
Frequently Asked Questions (FAQs) of RD Sharma Chapter 10 Class 9 Maths Exercise 10.3 Solutions
Ques 1- What is SAS congruence criterion?
Ans- If any two sides and the angle comprised between the sides of one triangle are equal to the corresponding two sides and an angle among the sides of the second triangle, then the two triangles are assumed to be congruent by the SAS ( Side-Angle-Side) rule.
Ques 2- Are vertical angles SAS?
Ans- One of the simplest ways to prove angles congruent is to understand the Vertical Angles Theorem. The vertical angle theorem signifies that vertical angles are congruent.
Ques 3- How to Prove Triangles Congruent using the SAS Postulate?
Ans- If two sides and the added angle of one triangle are congruent to two sides and the added angle of the other triangle, formerly the two triangles are congruent.
Ques 4- What is needed to prove SAS?
Ans- The Side Angle Side (abbreviated as SAS) declares that if two sides and the added angle of one triangle are congruent to two sides and the added angle of another triangle, formerly these two triangles are congruent.
Ques 5- What is SAS similarity criteria?
Ans- The SAS criterion for triangle similarity signifies that if two sides of one triangle are proportional (comparable) to two sides of the other triangle and their composed angles are congruent, then the triangles are similar.
