In this RD Sharma Chapter 10 Class 9 Maths Exercise 10.4 Solutions, we will discuss the Congruence Criterion – SSS (Side-Side-Side), which is based on the Class 9 Chapter 10 Congruent Triangle. According to the rules, two triangles are congruent if the three sides of one triangle are equivalent to the corresponding three sides of another triangle. In the article, we have planned the solutions systematically to keep in mind the understanding of Class 9 students.
In the following attached PDF, students will get the various types of questions related to the Congruence Criterion – SSS (Side-Side-Side). Our experts tried to make easy and stepwise solutions by using figures in each problem given in the PDF. The RD Sharma Chapter 10 Class 9 Maths Exercise 10.4 Solutions PDF is prepared with the help of RD Sharma, Previous Year’s Question Paper, and Text Book of Class 9. The PDF is free to access for the learners to practice for the exam and score well.
Learn about RD Sharma Class 9 Chapter 10 (Congruent Triangles)
Download RD Sharma Chapter 10 Class 9 Maths Exercise 10.4 Solutions PDF
Solutions for Class 9 Maths Chapter 10 Congruent Triangles Exercise 10.4
Important Definitions RD Sharma Chapter 10 Class 9 Maths Exercise 10.4 Solutions
In this exercise of Chapter 10, we will learn about the Criterion of Congruence – SSS (Side-Side-Side). Go down and look at the information regarding Criterion of Congruence – SSS (Side-Side-Side).
SSS (Side-Side-Side)
If all the three (3) sides of one triangle are equal to the corresponding three sides of the second (another) triangle, formerly, the two triangles are assumed to be congruent by the SSS (Side-Side-Side) rule.
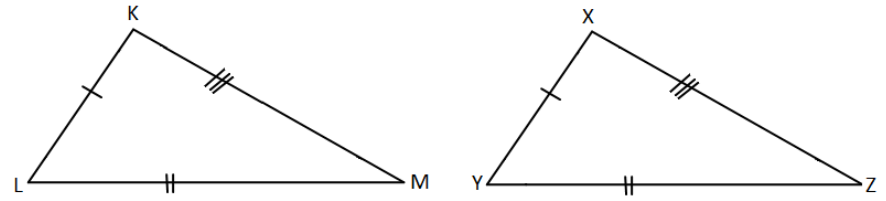
In the above-given figure,
Here in ∆KLM and ∆XYZ,
KL = XY, LM = YZ and KM = XZ.
Therefore, ∆KLM ≅ ∆XYZ.
Frequently Asked Questions (FAQs) of RD Sharma Chapter 10 Class 9 Maths Exercise 10.4 Solutions
Ques 1- What is side side side (SSS) congruence criterion?
Ans- The abbreviation of side-side-side is SSS. If two triangles both have all of the sides equal (if one triangle has side lengths p, q, r, then so does another triangle), they can be congruent.
Ques 2- Does SSS prove congruence?
Ans- Side-Side-Side is a rule applied to prove whether a provided set of triangles are congruent. The SSS rule declares that- If three sides of one triangle are equivalent to three sides of the other triangle, formerly, the triangles are congruent.
Ques 3- Why does SSS prove congruence?
Ans- The SSS Theorem- If the three sides of one triangle are equivalent to the three sides of the other triangle, the triangles are congruent.
Our proof, following that of Euclid, is based on representing one of the triangles and then proving that the other triangle is congruent to this study.
