
RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3: This exercise includes problems on the volume and surface area of a frustum of a right circular cone. Students can get the RD Sharma Class 10 Solutions prepared by Kopykitab’s experts for the primary objective of reinforcing ideas and problem-solving skills. Students can also get the RD Sharma Solutions for Class 10 Maths Chapter 16 Surface Areas And Volumes Exercise 16.3 PDF by clicking on the link below.
Download RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3 Free PDF
RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3
Access answers to RD Sharma Solutions Class 10 Maths Chapter 16 Exercise 16.3- Important Question with Answers
1. A bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs 1.20 per dm2.
Solution:
Given,
Diameter to top of bucket = 40 cm
So, the radius (r1) = 40/2 = 20 cm
Diameter of bottom part of the bucket = 20 cm
So, the radius (r2) = 30/2 = 10cm
Depth of the bucket (h) = 12 cm
Volume of the bucket = 1/3 π(r22+ r12 + r1 r2 )h
= π/3(202 + 102 + 20 × 10)12
= 8800 cm3
Now,
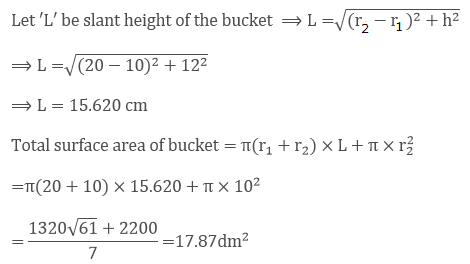
Given that the cost of tin sheet used for making bucket per dm2 = Rs 1.20
So, the total cost for 17.87dm2 = 1.20 × 17.87 = Rs 21.40
Therefore, the cost of tin sheet used for making the bucket is Rs 21.40
2. A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm and height 3 cm. Find the area of its whole surface and volume.
Solution:
Given,
Base diameter of cone (d1) = 20 cm
So the radius (r1) = 20/2 cm = 10 cm
Top diameter of Cone (d2) = 12 cm
So, the radius (r2) = 12/2 cm = 6 cm
Height of the cone (h) = 3 cm
Volume of the frustum of a right circular cone = 1/3 π(r22+ r12 + r1 r2 )h
= π/3(102 + 62 + 10 × 6)3
= 616 cm3
Let ‘L’ be the slant height of cone, then we know that
L = √(r1 – r21)2 + h2
L = √(10 – 6)2 + 32
L = √(16 + 9)
L = 5cm
So, the slant height of cone (L) = 5 cm
Thus,
Total surface area of the frustum = π(r1 + r2) x L + π r12 + π r22
= π(10 + 6) × 5 + π × 102 + π × 62
= π(80 + 100 + 36)
= π(216)
= 678.85 cm2
3. The slant height of the frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface of the frustum.
Solution:
Given,
Slant height of frustum of cone (l) = 4 cm
Let ratio of the top and bottom circles be r1 and r2
And given perimeters of its circular ends as 18 cm and 6 cm
⟹ 2πr1 = 18 cm; 2πr2 = 6 cm
⟹ πr1= 9 cm and πr2 = 3 cm
We know that,
Curved surface area of frustum of a cone = π(r1 + r2)l
= π(r1 + r2)l
= (πr1+πr2)l = (9 + 3) × 4 = (12) × 4 = 48 cm2
Therefore, the curved surface area of the frustum = 48 cm2
4. The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
Solution:
Given,
Perimeter of the upper end = 44 cm
2 π r1 = 44
2(22/7) r1 = 44
r1 = 7 cm
Perimeter of the lower end = 33 cm
2 π r2 = 33
2(22/7) r2 = 33
r2 = 21/4 cm
Now,
Let the slant height of the frustum of a right circular cone be L
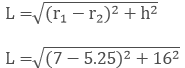
L = 16.1 cm
So, the curved surface area of the frustum cone = π(r1 + r2)l
= π(7 + 5.25)16.1
Curved surface area of the frustum cone = 619.65 cm3
Next,
The volume of the frustum cone = 1/3 π(r22+ r12 + r1 r2 )h
= 1/3 π(72+ 5.252 + (7) (5.25)) x 16
= 1898.56 cm3
Thus, volume of the cone = 1898.56 cm3
Finally, the total surface area of the frustum cone
= π(r1 + r2) x L + π r12 + π r22
= π(7 + 5.25) × 16.1 + π72 + π5.252
= π(7 + 5.25) × 16.1 + π(72 + 5.252) = 860.27 cm2
Therefore, the total surface area of the frustum cone is 860.27 cm2
5. If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket.
Solution:
Given,
Height of the conical bucket = 45 cm
Radii of the 2 circular ends of the conical bucket are 28 cm and 7 cm
So, r1 = 28 cm r2 = 7 cm
Volume of the conical bucket = 1/3 π(r12+ r22 + r1 r2 )h
= 1/3 π(282 + 72 + 28 × 7)45 = 15435π
Therefore, the volume/ capacity of the bucket is 48510 cm3.
We have provided complete details of RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3. If you have any queries related to CBSE Class 10, feel free to ask us in the comment section below.
FAQs on RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3
Where can I get RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3 Free PDF?
You can get RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3 Free PDF from the above article.
Where can I get the correct RD Sharma Solutions for Class 10 Maths Chapter 16 Exercise 16.3?
On the Kopykitab website, students can find appropriate and accurate RD Sharma Solutions for Class 10 Maths Chapter 16 Exercise 16.3. The best reference materials are RD Sharma textbooks, which give students and teachers a wide choice of sample questions to answer. The solutions are carefully crafted to ensure that students grasp the concepts and perform well on their board exams.
Is the RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3 available on the Kopykitab website?
Yes, the PDFs of RD Sharma Class 10 Solutions Chapter 16 Exercise 16.3 are available. These solutions are created in a unique method by Kopykitab’s expert faculty.
