RD Sharma Class 10 Solutions Chapter 2 VSAQS (Updated for 2021-22)

RD Sharma Class 10 Solutions Chapter 2 VSAQs: Students can download the RD Sharma Class 10 Solutions Chapter 2 VSAQs PDF to learn how to solve the questions in this exercise correctly. Students wishing to brush up their concepts can check the RD Sharma Solutions Class 10.

Access RD Sharma Class 10 Solutions Chapter 2 VSAQs PDF

Question 1.
Define a polynomial with real coefficients.
Solution: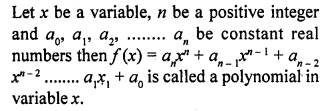

Question 2.
Define the degree of a polynomial.
Solution:
The exponent of the highest degree term in a polynomial is known as its degree. A polynomial of degree O is called a constant polynomial.

Question 3.
Write the standard form of a linear polynomial with real coefficients.
Solution:
ax + b is the standard form of a linear polynomial with real coefficients and a ≠ 0

Question 4.
Write the standard form of a quadratic polynomial with real coefficients.
Solution:
ax² + bx + c is a standard form of a quadratic polynomial with real coefficients and a ≠ 0.

Question 5.
Write the standard form of a cubic polynomial with real coefficients.
Solution:
ax³ + bx² + cx + d is a standard form of the cubic polynomial with real coefficients and a ≠ 0.

Question 6.
Define the value of a polynomial at a point.
Solution:
If f(x) is a polynomial and a is any real number then the real number obtained by replacing x by α in f(x) is called the value of f(x) at x = α and is denoted by f(α).

Question 7.
Define zero of a polynomial.
Solution:
A real number a is a zero of a polynomial f(x) if f(α) = 0.

Question 8.
The sum and product of the zeros of a quadratic polynomial are – 12 and -3 respectively. What is the quadratic polynomial?
Solution: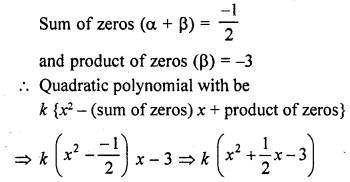

Question 9.
Write the family of quadratic polynomials having – 14 and 1 as its zeros.
Solution:

Question 10.
If the product of zeros of the quadratic polynomial f(x) = x² – 4x + k is 3, find the value of k.
Solution:
We know that a quadratic polynomial x² – (sum of zeros) x + product of zeros
In the given polynomial f(x) = x² – 4x + k is the product of zeros which is equal to 3
k = 3

Question 11.
If the sum of the zeros of a quadratic polynomial f(x) = kx² – 3x + 5 is 1, write the value of k.
Solution:
f (x) = kx² – 3x + 5
Here a = k, b = -3, c = 5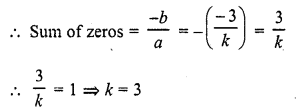

Question 12.
In the figure, the graph of a polynomial p (x) is given. Find the zeros of the polynomial.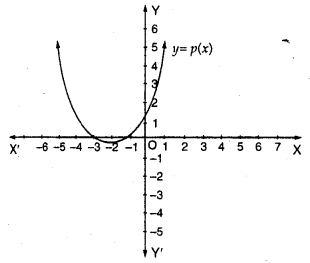

Solution:
The graph of the given polynomial meets the x-axis at -1 and -3
Zero will be -1 and -3
Zero of a polynomial is 3

Question 13.
The graph of a polynomial y = f(x) is given below. Find the number of real zeros of f (x).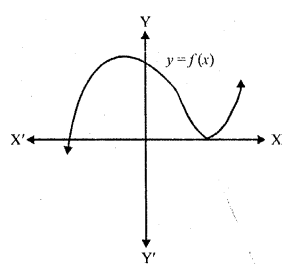

Solution:
The curve touches the x-axis at one point and also intersects at one point So the number of zeros will be 3, two equal, and one distinct

Question 14.
The graph of the polynomial f(x) = ax² + bx + c is as shown below (in the figure) write the signs of ‘a’ and b² – 4ac.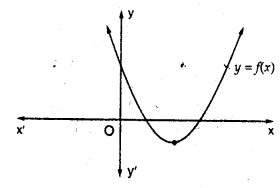

Solution:
The shape of the parabola is up to word a > 0
and b² – 4ac >0 i.e., both are positive.

Question 15.
The graph of the polynomial f(x) = ax² + bx + c is as shown in the figure write the value of b² – 4ac and the number of real zeros of f(x).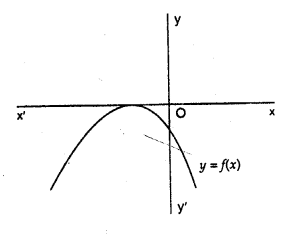

Solution:
The curve parabola touches the x-axis at one point
It has two equal zeros
b² – 4ac = 0

Question 16.
In Q. No. 14, write the sign of c
Solution:
The mouth of a parabola is upward and intersect the y-axis above the x-axis
c > 0

Question 17.
In Q. No. 15, write the sign of c.
Solution:
The mouth of the parabola is downward and intersects the y-axis below the x-axis
c < 0

Question 18.
The graph of a polynomial f (x) is as shown in the figure. Write the number of real zeros of f (x).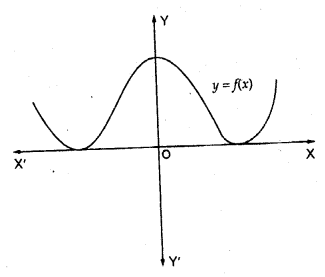

Solution:
The curves touch the x-axis at two distinct point
It has a pair of two equal zeros i.e., it has 4 real zeros

Question 19.
If x = 1, is a zero of the polynomial f(x) = x³ – 2x² + 4x + k, write the value of k.
Solution: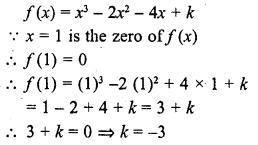

Question 20.
State division algorithm for polynomials.
Solution:
If f(x) is a polynomial and g (x) is a non zero polynomial, there exist two polynomials q (x) and r (x) such that
f(x) = g (x) x q (x) + r (x)
where r (x) = 0 or degree r (x) < degree g (x)
This is called division algorithm

Question 21.
Give an example of polynomials f(x), g (x), q (x) and r (x) satisfying f(x) = g (x) . q (x) + r (x), where degree r (x) = 0.
Solution:
f (x) = x³ + x² + x + 4
g (x) = x + 1
q (x) = x² + 1
r (x) = 3
is an example of f (x) = g (x) x q (x) + r (x)
where degree of r (x) is zero.

Question 22.
Write a quadratic polynomial, a sum of whose zeros is 2√3 and their product is 2.
Solution:
Sum of zeros = 2 √3
and product of zeros = 2
Quadratic polynomial will be f (x) = x2 – (sum of zeros) x + product of zeros
= x² – 2 √3 x + 2

Question 23.
If the fourth-degree polynomial is divided by a quadratic polynomial, write the degree of the remainder.
Solution:
Degree of the given polynomial = 4
and degree of divisor = 2
The degree of quotient will be 4 – 2 = 2
and degree of the remainder will be less than 2 In other words equal to or less than one degree

Question 24.
If f(x) = x³ + x² – ax + b is divisible by x² – x, write the value of a and b.
Solution: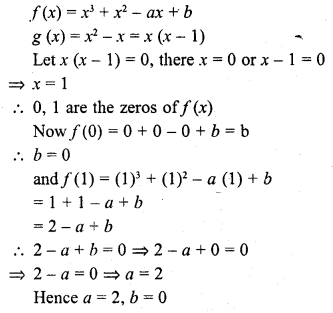

Question 25.
If a – b, a and a + b are zeros of the polynomial f(x) = 2x³ – 6x² + 5x – 7, write the value of a.
Solution: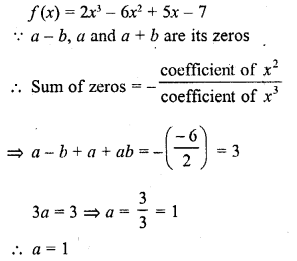

Question 26.
Write the coefficients of the polynomial p (z) = z⁵ – 2z² + 4.
Solution:
p (z) = z⁵ + oz⁴ + oz³ – 2z² + oz + 4
Coefficient of z⁵ = 1
Coefficient of z⁴ = 0
Coefficient of z³ = 0
Coefficient of z² = – 2
Coefficient of z = 0
Constant = 4

Question 27.
Write the zeros of the polynomial x² – x – 6. (C.B.S.E. 2008)
Solution: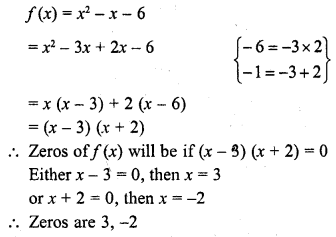

Question 28.
If (x + a) is a factor of 2x² + 2ax + 5x + 10, find a. (C.B.S.E. 2008)
Solution:
x + a is a factor of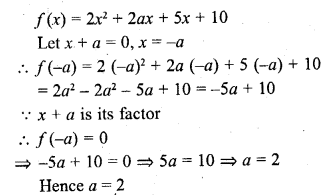

Question 29.
For what value of k, -4 is a zero of the polynomial x² – x – (2k + 2)? (CBSE 2009)
Solution: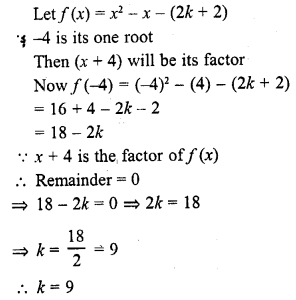

Question 30.
If 1 is a zero of the polynomial p (x) = ax² – 3 (a – 1) x – 1, then find the value of a.
Solution: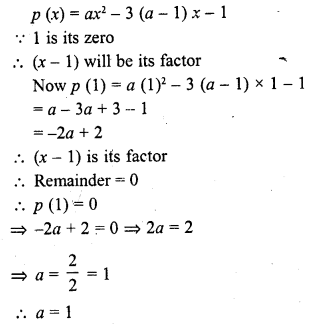

Question 31.
If α, β are the zeros of a polynomial such that α + β = -6 and α β = -4, then write the polynomial. [CBSE 2010]
Solution:

Question 32.
If α, β are the zeros of the polynomial 2y² + 7y + 5, write the value of α + β + αβ. [CBSE 2010]
Solution: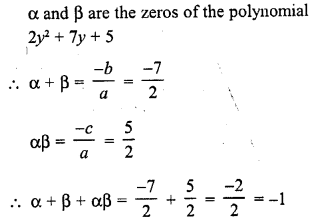

Question 33.
For what value of k, is 3 a zero of the polynomial 2x² + x + k ? [CBSE 2010]
Solution:
3 is a zero of f(x) = 2x² + x + k
It will satisfy the polynomial
f(x) = 0 ⇒ f(3) = 0
Now 2x² + x + k = 0
=> 2 (3)² + 3 + k = 0
=> 18 + 3 + k = 0
=> 21 + k = 0
=> k = -21

Question 34.
For what value of k, is -3 a zero of the polynomial x² + 11x + k ? [CBSE 2010]
Solution:
-3 is a zero of polynomial f(x) = x² + 11x + k
It will satisfy the polynomial
f (x) = 0 => f(-3) = 0
Now x² + 11x + k = 0
=> (-3)²+ 11 x (-3) + k = 0
⇒ 9 – 33 + k = 0
⇒ -24 + k = 0
⇒ k = 24

Question 35.
For what value of k, is -2 a zero of the polynomial 3x² + 4x + 2k ? [CBSE 2010]
Solution:
-2 is a zero of the polynomial
f(x) = 3x² + 4x + 2k
f(-2) = 0
=> 3 (-2)² + 4 (-2) + 2k = 0
=> 12 – 8 + 2k = 0
=> 4 + 2k = 0
=> 2k = -4
=> k = -2

Question 36.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f (x)?
Solution:
In a quadratic polynomial f(x) its degree is 2 and it can be factorized into two distinct linear factors.
f(x) has two distinct zeros

Question 37.
If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are coincident. (True / False)
Solution:
In a quadratic polynomial f(x), it is the square of a linear polynomial It has two zeros that are equal i.e. coincident
It is true

Question 38.
If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real zero. (True / False)
Solution:
A quadratic polynomial f(x) is not factorized into linear factors It has no real zeros It is true

Question 39.
If f(x) is a polynomial such that f(a) f(b) < 0, then what is the number of zeros lying between a and b?
Solution:
f(x) is a polynomial such that f(a) f(b) < 0
At least one of its zeros will be between a and b

Question 40.
If a graph of quadratic polynomial ax² + bx + c cuts the positive direction of the y-axis, then what is the sign of c?
Solution:
The graph of quadratic polynomial ax² + bx + c cuts positive direction of y-axis Then sign of constant term c will be also positive.

Question 41.
If the graph of quadratic polynomial ax² + bx + c cuts the negative direction of the y-axis, then what is the sign of c?
Solution:
The graph of quadratic polynomial ax² + bx + c cuts the negative side of the y-axis
Then the sign of constant term c will be negative.

We have provided complete details of RD Sharma Class 10 Solutions Chapter 2 VSAQs. If you have any queries related to CBSE Class 10, feel free to ask us in the comment section below.

FAQs on RD Sharma Class 10 Solutions Chapter 2 VSAQs