
RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4: If you are looking for a good help book for your Class 9 Maths exam, then start studying RD Sharma Solutions Class 9 Maths. There are solutions designed as per the urrent CBSE Syllabus. Subject matter experts have made sure that you understand RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4. To know more, read the whole blog.
Access answers of RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4
Question 1.
Give the geometric representations of the following equations.
(a) on the number line
(b) on the cartesian plane.
(i) x – 2
(ii) y + 3 = 0
(iii) y = 3
(iv) 2x + 9 = 0
(v) 3x – 5 = 0
Solution:
(i) x = 2
(i) on the number line![]()
(ii) x = 2 is a line parallel to 7-axis at a distance of 2 units to right of y-axis.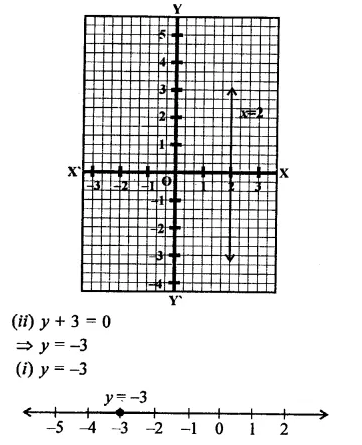
(ii) y = -3 is a line parallel to x-axis at a distance of 3 units below x-axis.
(iii) y = 3
(i) y = 3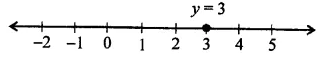
(ii) y = 3 is a line parallel to x-axis at a distance of 3 units above x-axis.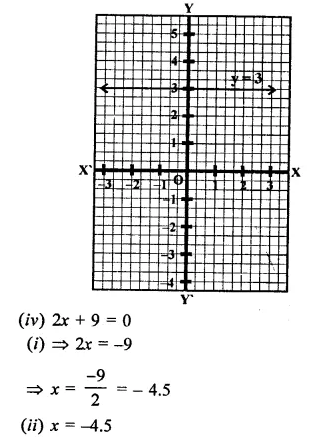
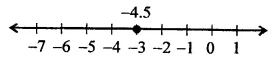
x = -4.5 is a line parallel to 7-axis at a distance of 4.5 units to left of y-axis.

(ii) x = 123 is a line parallel to y-axis at a distance of 123 unit to right side of y-axis.
Question 2.
Give the geometrical representation of 2x + 13 = 0 as an equation in
(i) One variable
(ii) Two variables
Solution:
(i) In one variable,
2x + 13 = 0
⇒ 2x = – 13
⇒ x = −132
is a line parallel to y-axis at a distance of -6 12 units on the left side of y-axis.
Question 3.
Solve the equation 3x + 2 = x -8, and represent on
(i) the number line
(ii) the Cartesian plane.
Solution:
3x + 2 = x – 8
⇒ 3x – x = -8 – 2
⇒ 2x = -10
⇒ x = −102 = -5
(i) on the number line s = -5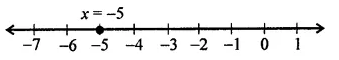
(ii) x = -5 is a line parallel to y-axis at a distance of 5 knot’s left of y-axis.
Question 4.
Write the equal of the line that is parallel to x-axis and passing through the points.
(i) (0, 3)
(ii) (0, -4)
(iii) (2, -5)
(iv) (3, 4)
Solution:
∵ A line parallel to x-axis will be of the type y = a
∴ (i) y = 3
(ii) y = -4
(iii) y = -5 and y = 4 are equations of the lines parallel to x-axis
Question 5.
Write the equation of the line that is parallel to y-axis and passing through the points.
(i) (4, 0)
(ii) (-2, 0)
(iii) (3, 5)
(iv) (-4, -3)
Solution:
∵ A line parallel to y-axis will be of the type x = a
∴ (i) x = 4, (ii) x = -2, x = 3 and x = -4 are the equations of the lines parallel to y-axis.
This is the complete blog on RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4. To know more about the CBSE Class 9 Maths exam, ask in the comments.
FAQs on RD Sharma Class 9 Solutions for Chapter 7 Exercise 7.4
From where can I download the PDF of RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4?
You can find the download link from the above blog.
How much does it cost to download the PDF of RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4?
You can download it for free.
Can I access the RD Sharma Class 9 Solutions Chapter 7 Exercise 7.4 PDF offline?
Once you have downloaded the PDF online, you can access it offline as well.
