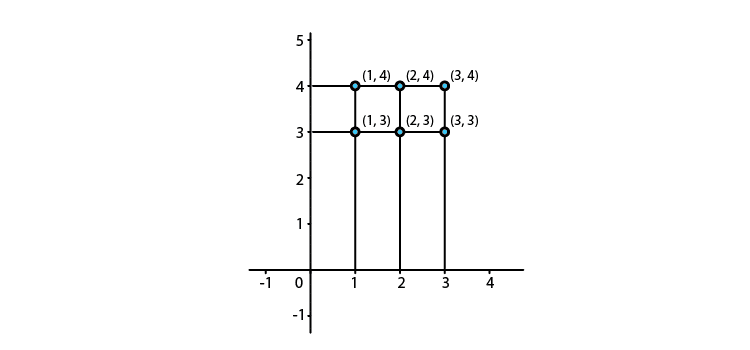RD Sharma Solutions Class 11 Maths Chapter 2: In this blog, we are going to talk about RD Sharma Solutions Class 11 Maths Chapter 2- Relations. For proper exam preparation, refer to RD Sharma Solutions Class 11 Maths Chapter 2. Get exam ready with RD Sharma Solutions Class 11 Maths Chapter 2.
Download RD Sharma Solutions Class 11 Maths Chapter 2 – Relations PDF
RD Sharma Solutions Class 11 Maths Chapter 2
Exercise-wise: RD Sharma Solutions Class 11 Maths Chapter 2 Relations
| RD Sharma Solutions Class 11 Chapter 2A |
| RD Sharma Solutions Class 11 Chapter 2B |
| RD Sharma Solutions Class 11 Chapter 2C |
RD Sharma Solutions Class 11 Chapter 2 Exercise 2.1
The RD Sharma Solutions for chapter 2 Exercise 2.1 is a basic exercise that starts with the introduction of relations, ordered pairs, Cartesian of products, and graphical representations of the same.
The Exercise 2.1 has some illustrative examples to help students understand each concept and then apply it together. The solutions provide a detailed step-by-step process of solving a question.
RD Sharma Solutions Class 11 Chapter 2 Exercise 2.2
The Exercise-2.2 is all about using some useful results to move ahead in the chapter. It includes working with theorems and its results for getting solutions quickly.
The exercise is very simple and small. Once you understand some basic terminologies, theorems, and results you can easily solve these questions.
RD Sharma Solutions Class 11 Chapter 2 Exercise 2.3
The Exercise-2.3 covers the relations with some practical application questions. It all covers all the concepts covered in the previous exercises to let students think and use all the concepts together when needed. The Exercise-2.3 solutions talk about Domain, Domain Range, and the inverse of a relation.
Access RD Sharma Solutions Class 11 Maths Chapter 2
EXERCISE 2.1 PAGE NO: 2.8
(1) (i) If (a/3 + 1, b – 2/3) = (5/3, 1/3), find the values of a and b.
(ii) If (x + 1, 1) = (3y, y – 1), find the values of x and y.
Solution:
Given:
(a/3 + 1, b – 2/3) = (5/3, 1/3)
By the definition of equality of ordered pairs,
Let us solve for a and b
a/3 + 1 = 5/3 and b – 2/3 = 1/3
a/3 = 5/3 – 1 and b = 1/3 + 2/3
a/3 = (5-3)/3 and b = (1+2)/3
a/3 = 2/3 and b = 3/3
a = 2(3)/3 and b = 1
a = 2 and b = 1
∴ Values of a and b are, a = 2 and b = 1
(ii) If (x + 1, 1) = (3y, y – 1), find the values of x and y.
Given:
(x + 1, 1) = (3y, y – 1)
By the definition of equality of ordered pairs,
Let us solve for x and y
x + 1 = 3y and 1 = y – 1
x = 3y – 1 and y = 1 + 1
x = 3y – 1 and y = 2
Since, y = 2 we can substitute in
x = 3y – 1
= 3(2) – 1
= 6 – 1
= 5
∴ Values of x and y are, x = 5 and y = 2
2. If the ordered pairs (x, – 1) and (5, y) belong to the set {(a, b): b = 2a – 3}, find the values of x and y.
Solution:
Given:
The ordered pairs (x, – 1) and (5, y) belong to the set {(a, b): b = 2a – 3}
Solving for first order pair
(x, – 1) = {(a, b): b = 2a – 3}
x = a and -1 = b
By taking b = 2a – 3
If b = – 1 then 2a = – 1 + 3
= 2
a = 2/2
= 1
So, a = 1
Since x = a, x = 1
Similarly, solving for second order pair
(5, y) = {(a, b): b = 2a – 3}
5 = a and y = b
By taking b = 2a – 3
If a = 5 then b = 2×5 – 3
= 10 – 3
= 7
So, b = 7
Since y = b, y = 7
∴ Values of x and y are, x = 1 and y = 7
3. If a ∈ {- 1, 2, 3, 4, 5} and b ∈ {0, 3, 6}, write the set of all ordered pairs (a, b) such that a + b = 5.
Solution:
Given: a ∈ {- 1, 2, 3, 4, 5} and b ∈ {0, 3, 6},
To find: the ordered pair (a, b) such that a + b = 5
Then the ordered pair (a, b) such that a + b = 5 are as follows
(a, b) ∈ {(- 1, 6), (2, 3), (5, 0)}
4. If a ∈ {2, 4, 6, 9} and b ∈ {4, 6, 18, 27}, then form the set of all ordered pairs (a, b) such that a divides b and a<b.
Solution:
Given:
a ∈ {2, 4, 6, 9} and b ∈{4, 6, 18, 27}
Here,
2 divides 4, 6, 18 and is also less than all of them
4 divides 4 and is also less than none of them
6 divides 6, 18 and is less than 18 only
9 divides 18, 27 and is less than all of them
∴ Ordered pairs (a, b) are (2, 4), (2, 6), (2, 18), (6, 18), (9, 18) and (9, 27)
5. If A = {1, 2} and B = {1, 3}, find A x B and B x A.
Solution:
Given:
A = {1, 2} and B = {1, 3}
A × B = {1, 2} × {1, 3}
= {(1, 1), (1, 3), (2, 1), (2, 3)}
B × A = {1, 3} × {1, 2}
= {(1, 1), (1, 2), (3, 1), (3, 2)}
6. Let A = {1, 2, 3} and B = {3, 4}. Find A x B and show it graphically
Solution:
Given:
A = {1, 2, 3} and B = {3, 4}
A x B = {1, 2, 3} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
Steps to follow to represent A × B graphically,
Step 1: One horizontal and one vertical axis should be drawn
Step 2: Element of set A should be represented in horizontal axis and on vertical axis elements of set B should be represented
Step 3: Draw dotted lines perpendicular to horizontal and vertical axes through the elements of set A and B
Step 4: Point of intersection of these perpendicular represents A × B
7. If A = {1, 2, 3} and B = {2, 4}, what are A x B, B x A, A x A, B x B, and (A x B) ∩ (B x A)?
Solution:
Given:
A = {1, 2, 3} and B = {2, 4}
Now let us find: A × B, B × A, A × A, (A × B) ∩ (B × A)
A × B = {1, 2, 3} × {2, 4}
= {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}
B × A = {2, 4} × {1, 2, 3}
= {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
A × A = {1, 2, 3} × {1, 2, 3}
= {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
B × B = {2, 4} × {2, 4}
= {(2, 2), (2, 4), (4, 2), (4, 4)}
Intersection of two sets represents common elements of both the sets
So,
(A × B) ∩ (B × A) = {(2, 2)}
EXERCISE 2.2 PAGE NO: 2.12
1. Given A = {1, 2, 3}, B = {3, 4}, C = {4, 5, 6}, find (A x B) ∩ (B x C).
Solution:
Given:
A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}
Let us find: (A × B) ∩ (B × C)
(A × B) = {1, 2, 3} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
(B × C) = {3, 4} × {4, 5, 6}
= {(3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
∴ (A × B) ∩ (B × C) = {(3, 4)}
2. If A = {2, 3}, B = {4, 5}, C = {5, 6} find A x (B ∪ C), (A x B) ∪ (A x C).
Solution:
Given: A = {2, 3}, B = {4, 5} and C = {5, 6}
Let us find: A x (B ∪ C) and (A x B) ∪ (A x C)
(B ∪ C) = {4, 5, 6}
A × (B ∪ C) = {2, 3} × {4, 5, 6}
= {(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(A × B) = {2, 3} × {4, 5}
= {(2, 4), (2, 5), (3, 4), (3, 5)}
(A × C) = {2, 3} × {5, 6}
= {(2, 5), (2, 6), (3, 5), (3, 6)}
∴ (A × B) ∪ (A × C) = {(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
A × (B ∪ C) = {(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
3. If A = {1, 2, 3}, B = {4}, C = {5}, then verify that:
(i) A x (B ∪ C) = (A x B) ∪ (A x C)
(ii) A x (B ∩ C) = (A x B) ∩ (A x C)
(iii) A x (B – C) = (A x B) – (A x C)
Solution:
Given:
A = {1, 2, 3}, B = {4} and C = {5}
(i) A × (B ∪ C) = (A × B) ∪ (A × C)
Let us consider LHS: (B ∪ C)
(B ∪ C) = {4, 5}
A × (B ∪ C) = {1, 2, 3} × {4, 5}
= {(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)}
Now, RHS
(A × B) = {1, 2, 3} × {4}
= {(1, 4), (2, 4), (3, 4)}
(A × C) = {1, 2, 3} × {5}
= {(1, 5), (2, 5), (3, 5)}
(A × B) ∪ (A × C) = {(1, 4), (2, 4), (3, 4), (1, 5), (2, 5), (3, 5)}
∴ LHS = RHS
(ii) A × (B ∩ C) = (A × B) ∩ (A × C)
Let us consider LHS: (B ∩ C)
(B ∩ C) = ∅ (No common element)
A × (B ∩ C) = {1, 2, 3} × ∅
= ∅
Now, RHS
(A × B) = {1, 2, 3} × {4}
= {(1, 4), (2, 4), (3, 4)}
(A × C) = {1, 2, 3} × {5}
= {(1, 5), (2, 5), (3, 5)}
(A × B) ∩ (A × C) = ∅
∴ LHS = RHS
(iii) A × (B − C) = (A × B) − (A × C)
Let us consider LHS: (B − C)
(B − C) = ∅
A × (B − C) = {1, 2, 3} × ∅
= ∅
Now, RHS
(A × B) = {1, 2, 3} × {4}
= {(1, 4), (2, 4), (3, 4)}
(A × C) = {1, 2, 3} × {5}
= {(1, 5), (2, 5), (3, 5)}
(A × B) − (A × C) = ∅
∴ LHS = RHS
4. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that:
(i) A x C ⊂ B x D
(ii) A x (B ∩ C) = (A x B) ∩ (A x C)
Solution:
Given:
A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}
(i) A x C ⊂ B x D
Let us consider LHS A x C
A × C = {1, 2} × {5, 6}
= {(1, 5), (1, 6), (2, 5), (2, 6)}
Now, RHS
B × D = {1, 2, 3, 4} × {5, 6, 7, 8}
= {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
Since, all elements of A × C is in B × D.
∴We can say A × C ⊂ B × D
(ii) A × (B ∩ C) = (A × B) ∩ (A × C)
Let us consider LHS A × (B ∩ C)
(B ∩ C) = ∅
A × (B ∩ C) = {1, 2} × ∅
= ∅
Now, RHS
(A × B) = {1, 2} × {1, 2, 3, 4}
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
(A × C) = {1, 2} × {5, 6}
= {(1, 5), (1, 6), (2, 5), (2, 6)}
Since, there is no common element between A × B and A × C
(A × B) ∩ (A × C) = ∅
∴ A × (B ∩ C) = (A × B) ∩ (A × C)
5. If A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}, find
(i) A x (B ∩ C)
(ii) (A x B) ∩ (A x C)
(iii) A x (B ∪ C)
(iv) (A x B) ∪ (A x C)5. If A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}, find
(i) A x (B ∩ C)
(ii) (A x B) ∩ (A x C)
(iii) A x (B ∪ C)
(iv) (A x B) ∪ (A x C)
Solution:
Given:
A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}
(i) A × (B ∩ C)
(B ∩ C) = {4}
A × (B ∩ C) = {1, 2, 3} × {4}
= {(1, 4), (2, 4), (3, 4)}
(ii) (A × B) ∩ (A × C)
(A × B) = {1, 2, 3} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
(A × C) = {1, 2, 3} × {4, 5, 6}
= {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(A × B) ∩ (A × C) = {(1, 4), (2, 4), (3, 4)}
(iii) A × (B ∪ C)
(B ∪ C) = {3, 4, 5, 6}
A × (B ∪ C) = {1, 2, 3} × {3, 4, 5, 6}
= {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}
(iv) (A × B) ∪ (A × C)
(A × B) = {1, 2, 3} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
(A × C) = {1, 2, 3} × {4, 5, 6}
= {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(A × B) ∪ (A × C) = {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}
6. Prove that:
(i) (A ∪ B) x C = (A x C) = (A x C) ∪ (B x C)
(ii) (A ∩ B) x C = (A x C) ∩ (B x C)
Solution:
(i) (A ∪ B) x C = (A x C) = (A x C) ∪ (B x C)
Let (x, y) be an arbitrary element of (A ∪ B) × C
(x, y) ∈ (A ∪ B) C
Since, (x, y) are elements of Cartesian product of (A ∪ B) × C
x ∈ (A ∪ B) and y ∈ C
(x ∈ A or x ∈ B) and y ∈ C
(x ∈ A and y ∈ C) or (x ∈ Band y ∈ C)
(x, y) ∈ A × C or (x, y) ∈ B × C
(x, y) ∈ (A × C) ∪ (B × C) … (1)
Let (x, y) be an arbitrary element of (A × C) ∪ (B × C).
(x, y) ∈ (A × C) ∪ (B × C)
(x, y) ∈ (A × C) or (x, y) ∈ (B × C)
(x ∈ A and y ∈ C) or (x ∈ B and y ∈ C)
(x ∈ A or x ∈ B) and y ∈ C
x ∈ (A ∪ B) and y ∈ C
(x, y) ∈ (A ∪ B) × C … (2)
From 1 and 2, we get: (A ∪ B) × C = (A × C) ∪ (B × C)
(ii) (A ∩ B) x C = (A x C) ∩ (B x C)
Let (x, y) be an arbitrary element of (A ∩ B) × C.
(x, y) ∈ (A ∩ B) × C
Since, (x, y) are elements of Cartesian product of (A ∩ B) × C
x ∈ (A ∩ B) and y ∈ C
(x ∈ A and x ∈ B) and y ∈ C
(x ∈ A and y ∈ C) and (x ∈ Band y ∈ C)
(x, y) ∈ A × C and (x, y) ∈ B × C
(x, y) ∈ (A × C) ∩ (B × C) … (1)
Let (x, y) be an arbitrary element of (A × C) ∩ (B × C).
(x, y) ∈ (A × C) ∩ (B × C)
(x, y) ∈ (A × C) and (x, y) ∈ (B × C)
(x ∈A and y ∈ C) and (x ∈ Band y ∈ C)
(x ∈A and x ∈ B) and y ∈ C
x ∈ (A ∩ B) and y ∈ C
(x, y) ∈ (A ∩ B) × C … (2)
From 1 and 2, we get: (A ∩ B) × C = (A × C) ∩ (B × C)
7. If A x B ⊆ C x D and A ∩ B ∈ ∅, Prove that A ⊆ C and B ⊆ D.
Solution:
Given:
A × B ⊆ C x D and A ∩ B ∈ ∅
A × B ⊆ C x D denotes A × B is subset of C × D that is every element A × B is in C × D.
And A ∩ B ∈ ∅ denotes A and B does not have any common element between them.
A × B = {(a, b): a ∈ A and b ∈ B}
∴We can say (a, b) ⊆ C × D [Since, A × B ⊆ C x D is given]
a ∈ C and b ∈ D
a ∈ A = a ∈ C
A ⊆ C
And
b ∈ B = b ∈ D
B ⊆ D
Hence proved.
EXERCISE 2.3 PAGE NO: 2.20
1. If A = {1, 2, 3}, B = {4, 5, 6}, which of the following are relations from A to B?
Give reasons in support of your answer.
(i) {(1, 6), (3, 4), (5, 2)}
(ii) {(1, 5), (2, 6), (3, 4), (3, 6)}
(iii) {(4, 2), (4, 3), (5, 1)}
(iv) A × B
Solution:
Given,
A = {1, 2, 3}, B = {4, 5, 6}
A relation from A to B can be defined as:
A × B = {1, 2, 3} × {4, 5, 6}
= {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) {(1, 6), (3, 4), (5, 2)}
No, it is not a relation from A to B. The given set is not a subset of A × B as (5, 2) is not a part of the relation from A to B.
(ii) {(1, 5), (2, 6), (3, 4), (3, 6)}
Yes, it is a relation from A to B. The given set is a subset of A × B.
(iii) {(4, 2), (4, 3), (5, 1)}
No, it is not a relation from A to B. The given set is not a subset of A × B.
(iv) A × B
A × B is a relation from A to B and can be defined as:
{(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6),(3, 4),(3, 5),(3, 6)}
2. A relation R is defined from a set A = {2, 3, 4, 5} to a set B = {3, 6, 7, 10} as follows: (x, y) R x is relatively prime to y. Express R as a set of ordered pairs and determine its domain and range.
Solution:
Relatively prime numbers are also known as co-prime numbers. If there is no integer greater than one that divides both (that is, their greatest common divisor is one).
Given: (x, y) ∈ R = x is relatively prime to y
Here,
2 is co-prime to 3 and 7.
3 is co-prime to 7 and 10.
4 is co-prime to 3 and 7.
5 is co-prime to 3, 6 and 7.
∴ R = {(2, 3), (2, 7), (3, 7), (3, 10), (4, 3), (4, 7), (5, 3), (5, 6), (5, 7)}
Domain of relation R = {2, 3, 4, 5}
Range of relation R = {3, 6, 7, 10}
3. Let A be the set of first five natural and let R be a relation on A defined as follows: (x, y) R x ≤ y
Express R and R-1 as sets of ordered pairs. Determine also
(i) the domain of R‑1
(ii) The Range of R.
Solution:
A is set of first five natural numbers.
So, A= {1, 2, 3, 4, 5}
Given: (x, y) R x ≤ y
1 is less than 2, 3, 4 and 5.
2 is less than 3, 4 and 5.
3 is less than 4 and 5.
4 is less than 5.
5 is not less than any number A
∴ R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 3), (3, 4), (3, 5), (4, 4), (4, 5), (5, 5)}
“An inverse relation is the set of ordered pairs obtained by interchanging the first and second elements of each pair in the original relation. If the graph of a function contains a point (a, b), then the graph of the inverse relation of this function contains the point (b, a)”.
∴ R-1 = {(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (2, 2), (3, 2), (4, 2), (5, 2), (3, 3), (4, 3), (5, 3), (4, 4), (5, 4) (5, 5)}
(i) Domain of R‑1 = {1, 2, 3, 4, 5}
(ii) Range of R = {1, 2, 3, 4, 5}
4. Find the inverse relation R-1 in each of the following cases:
(i) R= {(1, 2), (1, 3), (2, 3), (3, 2), (5, 6)}
(ii) R= {(x, y) : x, y ∈ N; x + 2y = 8}
(iii) R is a relation from {11, 12, 13} to (8, 10, 12} defined by y = x – 3
Solution:
(i) Given:
R= {(1, 2), (1, 3), (2, 3), (3, 2), (5, 6)}
So, R‑1 = {(2, 1), (3, 1), (3, 2), (2, 3), (6, 5)}
(ii) Given,
R= {(x, y): x, y ∈ N; x + 2y = 8}
Here, x + 2y = 8
x = 8 – 2y
As y ∈ N, Put the values of y = 1, 2, 3,…… till x ∈ N
When, y = 1, x = 8 – 2(1) = 8 – 2 = 6
When, y = 2, x = 8 – 2(2) = 8 – 4 = 4
When, y = 3, x = 8 – 2(3) = 8 – 6 = 2
When, y = 4, x = 8 – 2(4) = 8 – 8 = 0
Now, y cannot hold value 4 because x = 0 for y = 4 which is not a natural number.
∴ R = {(2, 3), (4, 2), (6, 1)}
R‑1 = {(3, 2), (2, 4), (1, 6)}
(iii) Given,
R is a relation from {11, 12, 13} to (8, 10, 12} defined by y = x – 3
Here,
x = {11, 12, 13} and y = (8, 10, 12}
y = x – 3
When, x = 11, y = 11 – 3 = 8 ∈ (8, 10, 12}
When, x = 12, y = 12 – 3 = 9 ∉ (8, 10, 12}
When, x = 13, y = 13 – 3 = 10 ∈ (8, 10, 12}
∴ R = {(11, 8), (13, 10)}
R‑1 = {(8, 11), (10, 13)}
5. Write the following relations as the sets of ordered pairs:
(i) A relation R from the set {2, 3, 4, 5, 6} to the set {1, 2, 3} defined by x = 2y.
(ii) A relation R on the set {1, 2, 3, 4, 5, 6, 7} defined by (x, y) ∈ R ⇔ x is relatively prime to y.
(iii) A relation R on the set {0, 1, 2,…,10} defined by 2x + 3y = 12.
(iv) A relation R form a set A = {5, 6, 7, 8} to the set B = {10, 12, 15, 16, 18} defined by (x, y) R x divides y.
Solution:
(i) A relation R from the set {2, 3, 4, 5, 6} to the set {1, 2, 3} defined by x = 2y.
Let A = {2, 3, 4, 5, 6} and B = {1, 2, 3}
Given, x = 2y where y = {1, 2, 3}
When, y = 1, x = 2(1) = 2
When, y = 2, x = 2(2) = 4
When, y = 3, x = 2(3) = 6
∴ R = {(2, 1), (4, 2), (6, 3)}
(ii) A relation R on the set {1, 2, 3, 4, 5, 6, 7} defined by (x, y) ∈ R ⇔ x is relatively prime to y.
Given:
(x, y) R x is relatively prime to y
Here,
2 is co-prime to 3, 5 and 7.
3 is co-prime to 2, 4, 5 and 7.
4 is co-prime to 3, 5 and 7.
5 is co-prime to 2, 3, 4, 6 and 7.
6 is co-prime to 5 and 7.
7 is co-prime to 2, 3, 4, 5 and 6.
∴ R ={(2, 3), (2, 5), (2, 7), (3, 2), (3, 4), (3, 5), (3, 7), (4, 3), (4, 5), (4, 7), (5, 2), (5, 3), (5, 4), (5, 6), (5, 7), (6, 5), (6, 7), (7, 2), (7, 3), (7, 4), (7, 5), (7, 6), (7, 7)}
(iii) A relation R on the set {0, 1, 2,…, 10} defined by 2x + 3y = 12.
Given,
(x, y) R 2x + 3y = 12
Where x and y = {0, 1, 2,…, 10}
2x + 3y = 12
2x = 12 – 3y
x = (12-3y)/2
When, y = 0, x = (12-3(0))/2 = 12/2 = 6
When, y = 2, x = (12-3(2))/2 = (12-6)/2 = 6/2 = 3
When, y = 4, x = (12-3(4))/2 = (12-12)/2 = 0/2 = 0
∴ R = {(0, 4), (3, 2), (6, 0)}
(iv) A relation R form a set A = {5, 6, 7, 8} to the set B = {10, 12, 15, 16, 18} defined by (x, y) ∈ R ⇔ x divides y.
Given,
(x, y) R x divides y
Where, x = {5, 6, 7, 8} and y = {10, 12, 15, 16, 18}
Here,
5 divides 10 and 15.
6 divides 12 and 18.
7 divides none of the value of set B.
8 divides 16.
∴ R = {(5, 10), (5, 15), (6, 12), (6, 18), (8, 16)}
6. Let R be a relation in N defined by (x, y) ∈ R ⇔ x + 2y = 8. Express R and R-1 as sets of ordered pairs.
Solution:
Given,
(x, y) R x + 2y = 8 where x ∈ N and y ∈ N
x + 2y= 8
x = 8 – 2y
Putting the values y = 1, 2, 3,…… till x ∈ N
When, y = 1, x = 8 – 2(1) = 8 – 2 = 6
When, y = 2, x = 8 – 2(2) = 8 – 4 = 4
When, y = 3, x = 8 – 2(3) = 8 – 6 = 2
When, y = 4, x = 8 – 2(4) = 8 – 8 = 0
Now, y cannot hold value 4 because x = 0 for y = 4 which is not a natural number.
∴ R = {(2, 3), (4, 2), (6, 1)}
R‑1 = {(3, 2), (2, 4), (1, 6)}
7. Let A = {3, 5} and B = {7, 11}. Let R = {(a, b): a ∈ A, b ∈ B, a-b is odd}. Show that R is an empty relation from A into B.
Solution:
Given,
A = {3, 5} and B = {7, 11}
R = {(a, b): a ∈ A, b ∈ B, a-b is odd}
On putting a = 3 and b = 7,
a – b = 3 – 7 = -4 which is not odd
On putting a = 3 and b = 11,
a – b = 3 – 11 = -8 which is not odd
On putting a = 5 and b = 7:
a – b = 5 – 7 = -2 which is not odd
On putting a = 5 and b = 11:
a – b = 5 – 11 = -6 which is not odd
∴ R = { } = Φ
R is an empty relation from A into B.
Hence proved.
8. Let A = {1, 2} and B = {3, 4}. Find the total number of relations from A into B.
Solution:
Given,
A= {1, 2}, B= {3, 4}
n (A) = 2 (Number of elements in set A).
n (B) = 2 (Number of elements in set B).
We know,
n (A × B) = n (A) × n (B)
= 2 × 2
= 4 [since, n(x) = a, n(y) = b. total number of relations = 2ab]
∴ Number of relations from A to B are 24 = 16.
9. Determine the domain and range of the relation R defined by
(i) R = {(x, x+5): x ∈ {0, 1, 2, 3, 4, 5}
(ii) R= {(x, x3): x is a prime number less than 10}
Solution:
(i) R = {(x, x+5): x ∈ {0, 1, 2, 3, 4, 5}
Given,
R = {(x, x+5): x ∈ {0, 1, 2, 3, 4, 5}
∴ R = {(0, 0+5), (1, 1+5), (2, 2+5), (3, 3+5), (4, 4+5), (5, 5+5)}
R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
So,
Domain of relation R = {0, 1, 2, 3, 4, 5}
Range of relation R = {5, 6, 7, 8, 9, 10}
(ii) R= {(x, x3): x is a prime number less than 10}
Given,
R = {(x, x3): x is a prime number less than 10}
Prime numbers less than 10 are 2, 3, 5 and 7
∴ R = {(2, 23), (3, 33), (5, 53), (7, 73)}
R = {(2, 8), (3, 27), (5, 125), (7, 343)}
So,
Domain of relation R = {2, 3, 5, 7}
Range of relation R = {8, 27, 125, 343}
10. Determine the domain and range of the following relations:
(i) R= {a, b): a ∈ N, a < 5, b = 4}
(ii) S= {a, b): b = |a-1|, a ∈ Z and |a| ≤ 3}
Solution:
(i) R= {a, b): a ∈ N, a < 5, b = 4}
Given,
R= {a, b): a ∈ N, a < 5, b = 4}
Natural numbers less than 5 are 1, 2, 3 and 4
a = {1, 2, 3, 4} and b = {4}
R = {(1, 4), (2, 4), (3, 4), (4, 4)}
So,
Domain of relation R = {1, 2, 3, 4}
Range of relation R = {4}
(ii) S= {a, b): b = |a-1|, a ∈ Z and |a| ≤ 3}
Given,
S= {a, b): b = |a-1|, a ∈ Z and |a| ≤ 3}
Z denotes integer which can be positive as well as negative
Now, |a| ≤ 3 and b = |a-1|
∴ a = {-3, -2, -1, 0, 1, 2, 3}
For, a = -3, -2, -1, 0, 1, 2, 3 we get,
S = {(-3, |-3 – 1|), (-2, |-2 – 1|), (-1, |-1 – 1|), (0, |0 – 1|), (1, |1 – 1|), (2, |2 – 1|), (3, |3 – 1|)}
S = {(-3, |-4|), (-2, |-3|), (-1, |-2|), (0, |-1|), (1, |0|), (2, |1|), (3, |2|)}
S = {(-3, 4), (-2, 3), (-1, 2), (0, 1), (1, 0), (2, 1), (3, 2)}
b = 4, 3, 2, 1, 0, 1, 2
So,
Domain of relation S = {0, -1, -2, -3, 1, 2, 3}
Range of relation S = {0, 1, 2, 3, 4}
11. Let A = {a, b}. List all relations on A and find their number.
Solution:
The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B. If n (A) = p and n (B) = q, then n (A × B) = pq.
So, the total number of relations is 2pq.
Now,
A × A = {(a, a), (a, b), (b, a), (b, b)}
Total number of relations are all possible subsets of A × A:
[{(a, a), (a, b), (b, a), (b, b)}, {(a, a), (a, b)}, {(a, a), (b, a)},{(a, a), (b, b)}, {(a, b), (b, a)}, {(a, b), (b, b)}, {(b, a), (b, b)}, {(a, a), (a, b), (b, a)}, {(a, b), (b, a), (b, b)}, {(a, a), (b, a), (b, b)}, {(a, a), (a, b), (b, b)}, {(a, a), (a, b), (b, a), (b, b)}]
n (A) = 2 ⇒ n (A × A) = 2 × 2 = 4
∴ Total number of relations = 24 = 16
Important Topics From RD Sharma Solutions Class 11 Maths Chapter 2
The chapter has only a few topics important being listed below:
- Relation
- Domain
- Domain Range
- Using results and theorems
Key Take Away From RD Sharma Solutions Class 11 Maths Chapter 2
- Understanding is the key.
- Do not learn answers or the questions for the ease of solving them.
- Analyze every problem you did wrong.
- Do not leave any concept in between. Go through again because everything you leave will create a void for further levels.
Access Other Important Chapters of RD Sharma Solutions Class 11 Maths
- Chapter 3 – Functions
- Chapter 4 – Measurement of Angles
- Chapter 5 – Trigonometric Functions
- Chapter 6 – Graphs of Trigonometric Functions
- Chapter 7 – Trigonometric Ratios of Compound Angles
- Chapter 8 – Transformation Formulae
- Chapter 9 – Trigonometric Ratios of Multiple and Sub Multiple Angles
- Chapter 10 – Sine and Cosine Formulae and Their Applications
- Chapter 11 – Trigonometric Equations
- Chapter 12 – Mathematical Induction
- Chapter 13 – Complex Numbers
- Chapter 14 – Quadratic Equations
- Chapter 15 – Linear Inequations
- Chapter 16 – Permutations
- Chapter 17 – Combinations
- Chapter 18 – Binomial Theorem
- Chapter 19 – Arithmetic Progressions
- Chapter 20 – Geometric Progressions
- Chapter 21 – Some Special Series
- Chapter 22 – Brief Review of Cartesian System of Rectangular Coordinates
- Chapter 23 – The Straight Lines
- Chapter 24 – The Circle
- Chapter 25 – Parabola
- Chapter 26 – Ellipse
- Chapter 27 – Hyperbola
- Chapter 28 – Introduction To 3D Coordinate Geometry
- Chapter 29 – Limits
- Chapter 30 – Derivatives
- Chapter 31 – Mathematical Reasoning
- Chapter 32 – Statistics
- Chapter 33 – Probability
Doing this much is sufficient for Relations. Do let us know if you have any queries. We would like to answer your queries.
All the best for your CBSE class 11 examinations.
FAQs on RD Sharma Solutions Class 11 Maths Chapter 2
Are the solutions of RD Sharma Solutions Class 11 Maths Chapter 2 reliable?
The solutions of RD Sharma Solutions Class 11 Maths Chapter 2 are prepared by Subject matter experts and hence very reliable.
Can I access the RD Sharma Solutions Class 11 Maths Chapter 2 PDF offline?
Yes, once you have downloaded the PDF online you can access it offline as well.
From where can I download the RD Sharma Solutions Class 11 Maths Chapter 2 PDF?
You can download the PDF from the above link.
How much does it cost to download the RD Sharma Solutions Class 11 Maths Chapter 2 PDF?
You can download the PDF of RD Sharma Solutions Class 11 Maths Chapter 2 for free.