RD Sharma Class 11 Solutions Chapter 33 Probability Exercise 33.3 (Updated for 2021-22)

RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.3: It is based on a set of axioms. Experts’ key objective is to provide RD Sharma Class 11 Solutions and thereby assist students, regardless of their intelligence level. To assist them in performing well on the board exams, the solutions are described and solved in easy to understand manner. Students can get RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.3 from the links provided below and save them for future use.

Download RD Sharma Class 11 Solutions Chapter 33 Probability Exercise 33.3 Free PDF

RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.3

Access RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.3- Important Question with Answers

1. Which of the following cannot be a valid assignment of probability for elementary events or outcomes of sample space S = {w₁, w₂, w₃, w₄, w₅, w₆, w₇}: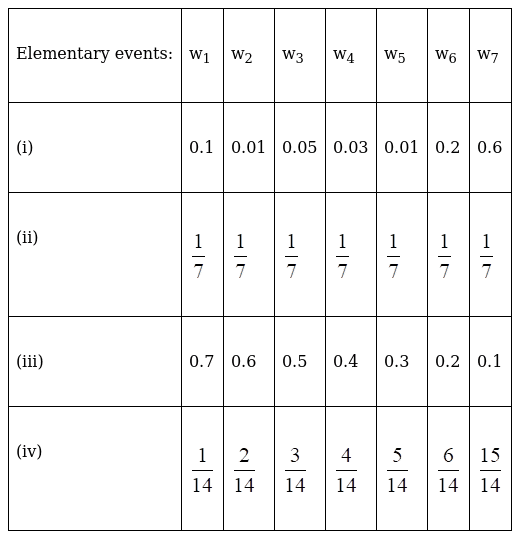

Solution:

For each event to be a valid assignment of probability.

The probability of each event in sample space should be less than 1 and the sum of probability of all the events should be exactly equal to 1.

(i) It is valid as each P (w_i) (for i=1 to 7) lies between 0 to 1 and sum of P (w₁) =1

(ii) It is valid as each P (w_i) (for i=1 to 7) lies between 0 to 1 and sum of P (w₁) =1

(iii) It is not valid as a sum of P (w_i) = 2.8 which is greater than 1

(iv) it is not valid as P (w₇) = 15/14 which is greater than 1

2. A die is thrown. Find the probability of getting:
(i) a prime number
(ii) 2 or 4
(iii) a multiple of 2 or 3

Solution:

Given: A die is thrown.

The total number of outcomes is six, n (S) = 6

By using the formula,

P (E) = favourable outcomes / total possible outcomes

(i) Let E be the event of getting a prime number

E = {2, 3, 5}

n (E) = 3

P (E) = n (E) / n (S)

= 3 / 6

= ½

(ii) Let E be the event of getting 2 or 4

E = {2, 4}

n (E) = 2

P (E) = n (E) / n (S)

= 2 / 6

= 1/3

(iii) Let E be the event of getting a multiple of 2 or 3

E = {2, 3, 4, 6}

n (E) = 4

P (E) = n (E) / n (S)

= 4 / 6

= 2/3

3. In a simultaneous throw of a pair of dice, find the probability of getting:
(i) 8 as the sum
(ii) a doublet
(iii) a doublet of prime numbers
(iv) an even number on first
(v) a sum greater than 9
(vi) an even number on first
(vii) an even number on one and a multiple of 3 on the other
(viii) neither 9 nor 11 as the sum of the numbers on the faces
(ix) a sum less than 6
(x) a sum less than 7
(xi) a sum more than 7
(xii) neither a doublet nor a total of 10
(xiii) odd number on the first and 6 on the second
(xiv) a number greater than 4 on each die
(xv) a total of 9 or 11
(xvi) a total greater than 8

Solution:

Given: a pair of dice has been thrown, so the number of elementary events in sample space is 6² = 36

n (S) = 36

By using the formula,

P (E) = favourable outcomes / total possible outcomes

(i) Let E be the event that the sum 8 appears

E = {(2, 6) (3, 5) (4, 4) (5, 3) (6, 2)}

n (E) = 5

P (E) = n (E) / n (S)

= 5 / 36

(ii) Let E be the event of getting a doublet

E = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}

n (E) = 6

P (E) = n (E) / n (S)

= 6 / 36

= 1/6

(iii) Let E be the event of getting a doublet of prime numbers

E = {((2, 2) (3, 3) (5, 5)}

n (E) = 3

P (E) = n (E) / n (S)

= 3 / 36

= 1/12

(iv) Let E be the event of getting a doublet of odd numbers

E = {(1, 1) (3, 3) (5, 5)}

n (E) = 3

P (E) = n (E) / n (S)

= 3 / 36

= 1/12

(v) Let E be the event of getting sum greater than 9

E = {(4,6) (5,5) (5,6) (6,4) (6,5) (6,6)}

n (E) = 6

P (E) = n (E) / n (S)

= 6 / 36

= 1/6

(vi) Let E be the event of getting even on first die

E = {(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)}

n (E) = 18

P (E) = n (E) / n (S)

= 18 / 36

= ½

(vii) Let E be the event of getting even on one and multiple of three on other

E = {(2,3) (2,6) (4,3) (4,6) (6,3) (6,6) (3,2) (3,4) (3,6) (6,2) (6,4)}

n (E) = 11

P (E) = n (E) / n (S)

= 11 / 36

(viii) Let E be the event of getting neither 9 or 11 as the sum

E = {(3,6) (4,5) (5,4) (5,6) (6,3) (6,5)}

n (E) = 6

P (E) = n (E) / n (S)

= 6 / 36

= 1/6

(ix) Let E be the event of getting sum less than 6

E = {(1,1) (1,2) (1,3) (1,4) (2,1) (2,2) (2,3) (3,1) (3,2) (4,1)}

n (E) = 10

P (E) = n (E) / n (S)

= 10 / 36

= 5/18

(x) Let E be the event of getting sum less than 7

E = {(1,1) (1,2) (1,3) (1,4) (1,5) (2,1) (2,2) (2,3) (2,4) (3,1) (3,2) (3,3) (4,1) (4,2) (5,1)}

n (E) = 15

P (E) = n (E) / n (S)

= 15 / 36

= 5/12

(xi) Let E be the event of getting more than 7

E = {(2,6) (3,5) (3,6) (4,4) (4,5) (4,6) (5,3) (5,4) (5,5) (5,6) (6,2) (6,3) (6,4) (6,5) (6,6)}

n (E) = 15

P (E) = n (E) / n (S)

= 15 / 36

= 5/12

(xii) Let E be the event of getting neither a doublet nor a total of 10

E′ be the event that either a double or a sum of ten appears

E′ = {(1,1) (2,2) (3,3) (4,6) (5,5) (6,4) (6,6) (4,4)}

n (E′) = 8

P (E′) = n (E′) / n (S)

= 8 / 36

= 2/9

So, P (E) = 1 – P (E′)

= 1 – 2/9

= 7/9

(xiii) Let E be the event of getting odd number on first and 6 on second

E = {(1,6) (5,6) (3,6)}

n (E) = 3

P (E) = n (E) / n (S)

= 3 / 36

= 1/12

(xiv) Let E be the event of getting greater than 4 on each die

E = {(5,5) (5,6) (6,5) (6,6)}

n (E) = 4

P (E) = n (E) / n (S)

= 4 / 36

= 1/9

(xv) Let E be the event of getting total of 9 or 11

E = {(3,6) (4,5) (5,4) (5,6) (6,3) (6,5)}

n (E) = 6

P (E) = n (E) / n (S)

= 6 / 36

= 1/6

(xvi) Let E be the event of getting total greater than 8

E = {(3,6) (4,5) (4,6) (5,4) (5,5) (5,6) (6,3) (6,4) (6,5) (6,6)}

n (E) = 10

P (E) = n (E) / n (S)

= 10 / 36

= 5/18

4. In a single throw of three dice, find the probability of getting a total of 17 or 18

Solution:

Given: The dices are thrown.

By using the formula,

P (E) = favourable outcomes / total possible outcomes

The total number of possible outcomes is 6³=216

So, n (S) = 216

Let E be the event of getting a total of 17 or 18

E = {(6, 6, 5) (6, 5, 6) (5, 6, 6) (6, 6, 6)}

n (E) = 4

P (E) = n (E) / n (S)

= 4 / 216

= 1/54

5. Three coins are tossed together. Find the probability of getting:
(i) exactly two heads
(ii) at least two heads
(iii) at least one head and one tail

Solution:

Given: Three coins are tossed together.

By using the formula,

P (E) = favourable outcomes / total possible outcomes

Total number of possible outcomes is 2³ = 8

(i) Let E be the event of getting exactly two heads

E = {(H, H, T) (H, T, H) (T, H, H)}

n (E) = 3

P (E) = n (E) / n (S)

= 3 / 8

(ii) Let E be the event of getting at least two heads

E= {(H, H, T) (H, T, H) (T, H, H) (H, H, H)}

n (E)=4

P (E) = n (E) / n (S)

= 4 / 8

= ½

(iii) Let E be the event of getting at least one head and one tail

E = {(H, T, T) (T, H, T) (T, T, H) (H, H, T) (H, T, H) (T, H, H)}

n (E) = 6

P (E) = n (E) / n (S)

= 6 / 8

= ¾

6. What is the probability that an ordinary year has 53 Sundays?

Solution:

Given: A year which includes 52 weeks and one day.

By using the formula,

P (E) = favourable outcomes / total possible outcomes

So, we now have to determine the probability of that one day being Sunday

The total number of possible outcomes is 7

n(S) = 7

E = {M, T, W, T, F, S, SU}

n (E) = 1

P (E) = n (E) / n (S)

= 1 / 7

7. What is the probability that a leap year has 53 Sundays and 53 Mondays?

Solution:

Given: A leap year which includes 52 weeks and two days

By using the formula,

P (E) = favourable outcomes / total possible outcomes

So, we now have to determine the probability of that remaining two days is Sunday and Monday

S = {MT, TW, WT, TF, FS, SSu, SuM}

n (S) = 7

E= {SuM}

n (E) = 1

P (E) = n (E) / n (S)

= 1 / 7

Probability Ex 33.3 Q8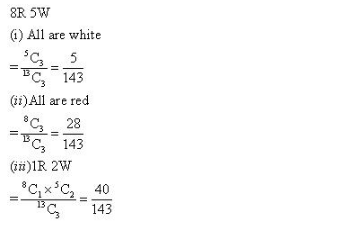

Probability Ex 33.3 Q9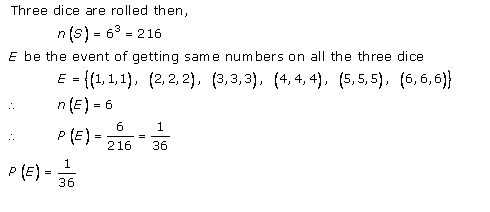

Probability Ex 33.3 Q10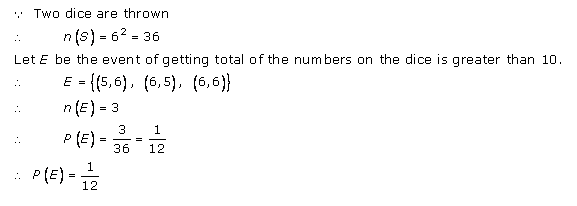

Probability Ex 33.3 Q11




Probability Ex 33.3 Q12

Probability Ex 33.3 Q13

Probability Ex 33.3 Q14

Probability Ex 33.3 Q15

Probability Ex 33.3 Q16


Probability Ex 33.3 Q17

Probability Ex 33.3 Q18

Probability Ex 33.3 Q19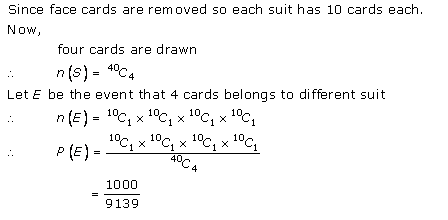

Probability Ex 33.3 Q20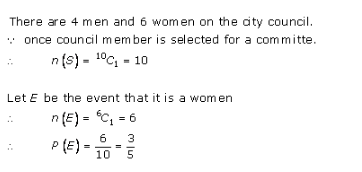

Probability Ex 33.3 Q21


Probability Ex 33.3 Q22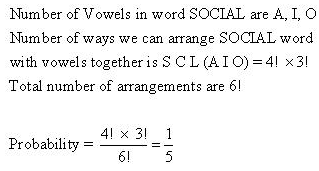

Probability Ex 33.3 Q23

Probability Ex 33.3 Q24

Probability Ex 33.3 Q25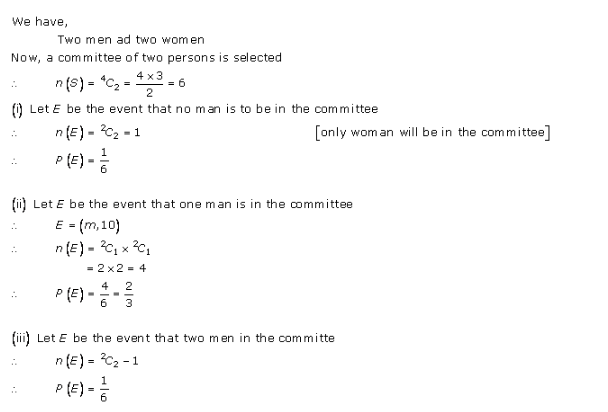

Probability Ex 33.3 Q26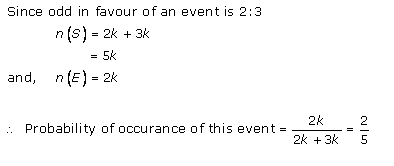

Probability Ex 33.3 Q27

Probability Ex 33.3 Q28

Probability Ex 33.3 Q29

Probability Ex 33.3 Q30

Probability Ex 33.3 Q31

Probability Ex 33.3 Q32

Probability Ex 33.3 Q33

Probability Ex 33.3 Q34


Probability Ex 33.3 Q35

Probability Ex 33.3 Q36

Probability Ex 33.3 Q37

Probability Ex 33.3 Q38


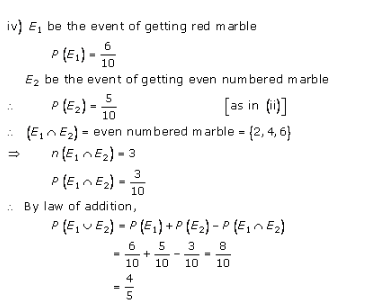
Probability Ex 33.3 Q39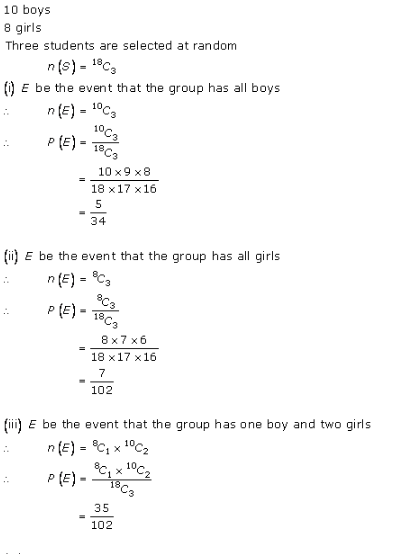


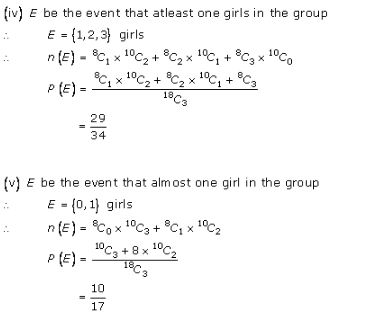
Probability Ex 33.3 Q40

Probability Ex 33.3 Q41

Probability Ex 33.3 Q42

Probability Ex 33.3 Q43

Probability Ex 33.3 Q44

Probability Ex 33.3 Q45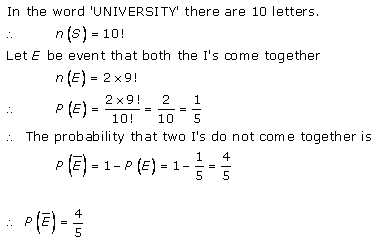

We have provided complete details of RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.3. If you have any queries related to CBSE Class 11, feel free to ask us in the comment section below.

FAQs on RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.3